Ejercicios y ejemplos con funciones en general:

Expresar mediante una fórmula la función que asocia a cada número:

a) Su cuádruplo.

     La función es: f (x) = 4x.

b) Un número 2 unidades mayor.

     La función es: f (x) = x + 2.

c) Su mitad menos 1.

     La función es: f (x) = x/2 − 1.

d) El cuadrado del número que es una unidad menor.

     La función es: f (x) = (x − 1)²

Veamos algunos otros ejemplos de funciones:

1) El volumen de un gas está determinado por la presión (a temperatura constante), esta relación viene dada por la ley de Boyle-Mariotte:

donde v representa el volumen del gas en litros, p es la presión en atmósferas  y c es una constante de proporcionalidad.

Se observa que al variar la presión a la que está sometido el gas varía el volumen; es decir, los valores del volumen dependen de los valores de la presión del gas y para cada valor de la presión existe un único valor del volumen.

2) El área  A del círculo depende de la longitud de su radio r y está dada por la fórmula:

Si se conoce el valor del radio se puede conocer el valor del área del círculo.

3) Dada la función  f(x) = 5x² + 2

Encontrar el valor de la función para cuando x = 2.

Para calcular la imagen de un elemento bajo la función  f, se reemplaza dicho elemento en el lugar de la variable, así para  x = 2

                                            f(2) = 5(2)²  + 2

                                            f(2) = 22

por lo tanto cuando x = 2, se tiene que  f(2) = 22.

Un problema resuelto

El precio de arrendar un auto es de 15 dólares más 0,20 de dólar por kilómetro recorrido.

a) Hallar la fórmula que expresa el costo del arriendo en función del número de los kilómetros recorridos.

b) ¿Cuánto hay que pagar si se han recorrido 50 kilómetros?

c) Si han cobrado 53 dólares ¿cuántos kilómetros se han recorrido?

Veamos:

a) Si llamamos x al número de kms recorridos, la fórmula de la función es f (x) = 15 + 0,2x.

b) x = 50  entonces

 f (50) = 15 + 0,2 • 50 = 25

Hay que pagar 25 dólares.

c) f (x) = 53  entonces

15 + 0,2x = 53 entonces x = 190

Se han recorrido 190 km.

Álgebra de funciones

Suma, resta, multiplicación y división de funciones

Sean f y g dos funciones cualesquiera.

Se define 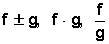 como

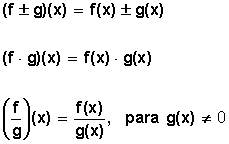
Ejemplos:

Suma de funciones

Sean las funciones

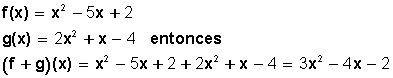
Resta de funciones

Producto de funciones

Sean las funciones

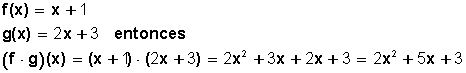
División de funciones

Sean las funciones

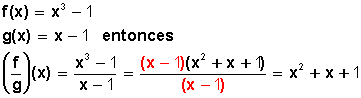
Nótese que hemos factorizado por (x − 1)