Ángulos de un triángulo: Los ángulos que se forman en un triángulo se relacionan entre sí cumpliendo con las siguientes propiedades o características:

1.- La suma de los ángulos internos de un triágulo es igual a dos ángulos rectos; es decir, suman 180º. En la figura, α + γ + ε = 180º. Recordar que γ = β  y que ε = δ por ser ángulos alternos internos.

2.- La suma de los ángulos agudos de un triángulo rectángulo es igual a 90º. En la figura, α + β = 90º

3.- En todo triángulo, la medida de un ángulo externo es igual a la suma de las medidas de los ángulos internos no contiguos (opuestos). En la figura, β = α + ε

4.- En todo triángulo la medida de un ángulo externo es mayor que la de cualquier ángulo interior no adyacente. En la figura, β > (es mayor que) α β > (es mayor que) e

5.- La suma tres ángulos exteriores de cualquier triángulo vale cuatro ángulos rectos; es decir, suman 360º. En la figura, α + β + γ = 360º

Triángulos :  

¿ Qué es un triángulo? Es un polígono de tres lados y tres ángulos.

¿ Qué es un triángulo? Es un polígono de tres lados y tres ángulos.

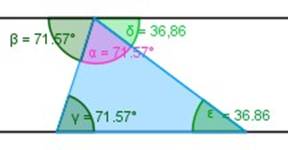
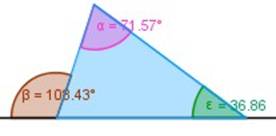
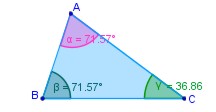
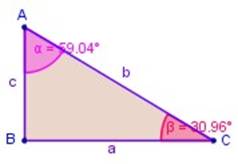
La suma de los ángulos interiores de cualquier triángulo es 180º Triángulo ABC: Tiene tres lados: AB, BC, CA Tiene tres vértices: A, B, C Tiene tres ángulos: ∠ ABC, ∠ BCA, ∠ CAB

¿Cómo se clasifican los triángulos?

Los triángulos se pueden clasificar según:

Las medidas de sus lados

Las medidas de sus ángulos

Según las medidas de sus lados pueden ser, triángulo:

Equilátero

Isósceles

Escaleno

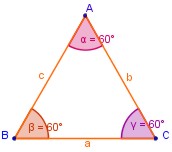
Triángulo equilátero: Es el que tiene sus tres lados de igual medida y sus tres ángulos de igual medida, cada uno de los cuales mide 60º. Los lados a, b y c tienen igual medida. Esto se puede escribir también de la siguiente manera: AB =  BC = CA Los ángulos tienen igual medida, es decir:  ∠ ABC = ∠ BCA  = ∠ CAB  =  60º Recuerda que siempre la letra que está en el medio indica el vértice donde se ubica el ángulo.

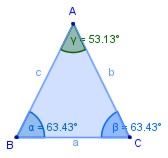
Triángulo isósceles: Es el que tiene dos lados de igual medida, por lo tanto, tiene dos ángulos de igual medida. trazo AB = trazo AC ∠ ABC = ∠ BCA

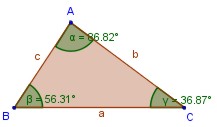
Triángulo escaleno: Es el que tiene todos sus lados de distinta medida y, por lo tanto, sus ángulos también son de distinta medida.

Según la medida de sus ángulos, un triángulo puede ser:

Triángulo acutángulo: Es el que tiene sus tres ángulos agudos; es decir, sus ángulos miden más de 0º y menos de 90º.  — — — AB AC BC ∠ ABC ∠ BCA ∠ CAB

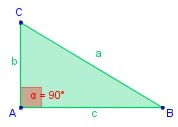
Triángulo rectángulo: Es el que tiene un ángulo recto; es decir, un ángulo mide 90º ∠ CAB  =  90º

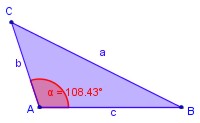
Triángulo obtusángulo: Es el que tiene un ángulo obtuso; o sea, un ángulo que mide más de 90º y menos de 180º. ∠ CAB  obtuso (mayor que 90º y menor que 180º)

Es importante tener presente que pueden combinarse ambas clasificaciones, según sus lados y según sus ángulos. Con esta información se pueden descubrir todas las propiedades implícitas en el nombre.

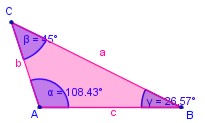	Tiene un ángulo obtuso y dos agudos distintos y tres lados distintos
Triángulo obtusángulo escaleno

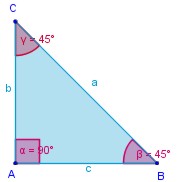	Tiene un ángulo de 90° y dos agudos iguales de 45° y dos lados iguales
Triángulo rectángulo isósceles