Geometría: 

1. Figuras geométricas:En la geometría, como disciplina, se distinguen componentes tales como el plano, el punto, la línea -recta, curva, quebrada-, la superficie, el segmento y otros de cuya combinación nacen todas las figuras geométricas.Entonces, una figura geométrica (también se la puede denominar lugar geométrico)  corresponde a un espacio cerrado por líneas o por superficies.

Las figuras geométricas de lados rectos se denominan polígonos y las figuras de lados curvos se denominan círculo y circunferencia y corresponden también a polígonos.

Es importante recordar que las formas sólidas o tridimensionales corresponden a los cuerpos geométricos y se denominan poliedros, como el cubo y la pirámide, y a los cuerpos redondos, como la esfera y el cilindro.

Según las características de las figuras geométricas (polígonos) se pueden establecer varias  clasificaciones. 

Según la medida de sus lados y ángulos, los polígonos pueden ser regulares e irregulares.

Un polígono es regular si todos sus lados poseen la misma longitud y si todos sus ángulos son iguales.

Ejemplos:

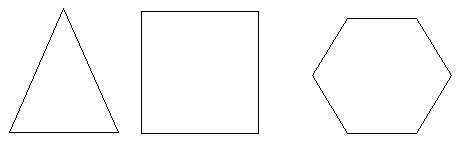Polígonos regulares

Un polígono es irregular si todos sus lados tienen longitudes diferentes al igual que la medida de sus ángulos.

Ejemplos:

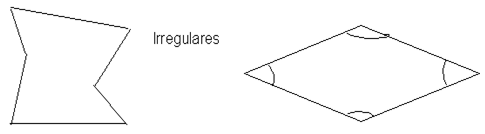Lados diferentes	Ángulos diferentes

De acuerdo con sus ángulos interiores, los polígonos pueden ser convexos y cóncavos.

Un polígono es convexo cuando todos sus ángulos interiores son menores a 180°

Ejemplo:

En el polígono ABCDE cada uno de sus ángulos interiores es menor de 180º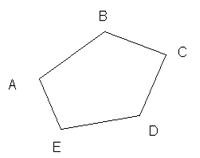

Un polígono es cóncavo, si tiene al menos un ángulo interior mayor de 180 °

Ejemplo:

El ángulo interior T del polígono RSTU es mayor de 180ª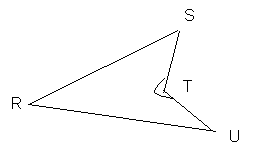

Ahora bien, según el número de lados que posean (el número de lados es igual al número de ángulos que tiene la figura) los polígono se pueden clasificar de la siguiente manera:

Nombre	Número de lados
Triángulo	3
Cuadrilátero	4
Pentágono	5
Hexágono	6
Heptágono	7
Octágono	8
Eneágono	9
Decágono	10
Undecágono	11
Dodecágono	12

Los demás polígonos simplemente se nombran indicando el número de lados que lo forman; polígono de trece lados, de catorce lados, etc., a excepción del polígono de veinte lados que también recibe un nombre específico (icoságono).

Triángulos:

Veamos en seguida lo referente al polígono de tres lados, llamado triángulo.

Los triángulos se clasifican según la medida de sus lados en:

Triángulo equilátero: el que tiene sus 3 lados iguales.

Triángulo isósceles:  el que tiene 2 de sus lados de igual medida.

Triángulo escaleno: el que tiene sus 3 lados de distinta medida.

Los triángulos también se pueden clasificar según la medida de sus ángulos en:     

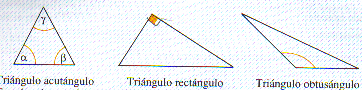
Triángulo acutángulo: el que tiene sus 3 ángulos agudos (menores de 90º)

Triángulo rectángulo: el que tiene 1 ángulo recto (90º)

Triángulo obtusángulo: el que tiene 1 ángulo obtuso (mayor de 90º y menos que 180º)

Cuadriláteros:

Otro de los polígonos muy populares son los cuadriláteros, los cuales se clasifican en:

Paralelogramos: son aquellos que tiene 2 pares de lados paralelos (cuadrado, rectángulo, rombo y romboide)

Trapecios: son aquellos que tienen 1 par de lados paralelos

trapecio isósceles: 2 lados de igual medida, 2 ángulos basales iguales

trapecio trisolátero: 3 lados de igual medida, 2 pares de ángulos basales iguales

trapecio rectángulo: ángulos basales rectos (90º)

trapecio escaleno: lados y ángulos de distinta medida

Trapezoides: No tienen lados paralelos

trapezoide simétrico: 2 lados de igual medida

trapezoide asimétrico: todos los lados de distinta medida

Conocer las características de los polígonos ayuda para el estudio de muchos temas como perímetros y áreas entre otros.

4. Números enteros:En la matemática moderna el conjunto de los números enteros (Z) abarca todos los enteros tanto negativos como positivos, y llega hasta el infinito hacia ambos lados de una recta numérica, por tanto, en rigor no existe un comienzo, salvo que como tal se considere el CERO (el cual agregado al conjunto de los números naturales forma el conjunto de los Cardinales).

Operaciones en Z (con enteros positivos y negativos)

Para poder realizar las operaciones en el conjunto de los números enteros (Z) debes memorizar las siguientes reglas (son fáciles; sólo requieren de práctica).

Suma en Z (Conjunto de Números Enteros positivos y negativos):

Existen únicamente dos casos: números de igual signo y números con signo distinto. Las reglas a memorizar son las siguientes:

a) Números de igual signo: Cuando dos números tiene igual signo se debe sumar y conservar el signo.

Ejemplos :        – 3   +  – 8  =   – 11      ( sumo y conservo el signo)

                         12   +   25  =   37       ( sumo y conservo el signo)

b) Números con distinto signo: Cuando dos números tienen distinto signo se debe restar y conservar el signo del número que tiene mayor valor absoluto (recuerda que el valor absoluto son unidades de distancia, lo cual significa que se debe considerar el número sin su signo).

Ejemplo:          – 7   +   12   =   5    (tener 12 es lo mismo que tener  +12, por lo tanto, los números son de distinto signo y se deben restar: 12  –  7  =   5 ¿con cuál signo queda? El valor absoluto de –7 es 7 y el valor absoluto de  +12 es 12, por lo tanto, el número que tiene mayor valor absoluto es el 12; debido a esto el resultado es un número positivo).

                    5   +   – 51   =   – 46   ( es negativo porque el 51 tiene mayor valor absoluto)

                   – 14  +   34   =    20

Resta en Z

Para restar dos números o más, es necesario realizar dos cambios de signo (uno después del otro) porque de esta manera la resta se transforma en suma y se aplican las reglas mencionadas anteriormente. Son dos los cambios de signo que deben hacerse:

a)         Cambiar el signo de la resta en suma 

b)         Cambiar el signo del número que está a la derecha del signo de operación por su signo contrario

Ejemplo 1:

     –3  –  10   

a) cambiamos el signo de resta por el de suma:

  –3    +  10 

b) cambiamos el signo del número que está a la derecha del signo de operación (que ahora es el +):

– 3 + – 10 =    –13   ( signos iguales se suma y conserva el signo)

Ejemplo 2:

19  –   – 16 

a) cambiamos el signo de resta por el de suma:

19 + –16

b) cambiamos el signo del número que está a la derecha (– 16) del signo de operación (que ahora es el +):

19 + + 16 =   19   +    16    =    35

Multiplicación y División en Z

La regla que se utiliza es la misma para multiplicar que para dividir. ¿CÓMO SE HACE? Multiplico los números y luego multiplico los signos de acuerdo a la siguiente tabla:

+   •    +    =    +

–   •   –     =    +

+   •   –     =   –

–  •   +     =   –

Ejemplos:   – 5   •    – 10   =    50    (  5  •   10   =    50 ;   –  •   –   =   + )

                     12  •    – 4    =   – 48    (  12 •   4   =     48;:    + •  –   =   – )

Siempre se deben multiplicar o dividir los números y luego aplicar las reglas de signos para dichas operaciones (las reglas de signos para la suma son para la suma y no deben ser confundidos con los de estas otras operaciones).

Suma y resta con números enteros 

multiplicación y división con números enteros 

Números Decimales :Los números decimales pueden escribirse de dos maneras: como fracción o bien en notación decimal.

Ejemplo:

3 / 10	=	0,3
Fracción		Notación decimal

Los números decimales pueden sumarse, restarse, multiplicarse y dividirse.

Adición y sustracción:

Para sumar o restar números decimales escritos con notación decimal se siguen los siguientes pasos:

1. Se anotan los números en forma vertical, es decir, se anotan hacia abajo, de modo que las comas queden en la misma columna. Siempre se debe colocar el número mayor arriba.

 Ejemplo:    

3,721	+	2,08		3,721
			+	2,08

2. Si los números que se ordenaron no tienen la misma cantidad de cifras decimales, se agregan a la derecha todos los ceros necesarios para que tengan igual cantidad.

Ejemplo:

	3, 721
+	2, 080

3. Se suma o resta en forma normal, luego se baja la coma (bajo su columna) y se agrega al resultado.

Ejemplo:

	3, 721			2, 867
+	2, 080		–	1, 344
	5, 801			1, 523

Suma con decimales :

Resta con decimales :

Multiplicación de un número decimal por un número natural: los pasos son los siguientes:

1. Se resuelve la multiplicación sin considerar la coma

Ejemplo:

1,322	•	2
2644

2. Una vez que se hizo la multiplicación, se  cuentan cuantos espacios después de la coma (hacia la derecha) están ocupados, y a partir del último número del resultado se cuentan hacia la izquierda los mismos espacios, y se coloca la coma.

Ejemplo:

1,322	•	2
2,644

Los espacios decimales ocupados son tres (los espacios decimales son los números que están detrás de la coma) . En el resultado, se cuentan  tres espacios desde el 4 al 6, y se coloca la coma

Multiplicación con decimales :

División: Los pasos son:

1.    Se resuelve la división de la forma acostumbrada.

Ejemplo:

	19	÷	5	=	3
–	15
	4

2. Como el resto es 4 (debe ser un número distinto de cero), se puede continuar dividiendo. Para esto se agrega una coma en el dividendo y un cero en el divisor.

	19	÷	5	=	3,
–	15
	4	0

3. Se continúa dividiendo y agregando un cero al resto todas las veces que se quiere; de esto depende el número de decimales que se quiera obtener.

	19	÷	5	=	3,8
–	15
	4	0
		40
		0

División con decimales :

Notación de mayor a menor:

Si dos o más números decimales tienen un entero del mismo valor, será mayor aquel que tenga el primer número mayor después de la coma; y si este es igual, será mayor aquel que tenga el siguiente número más grande..

Ejemplos (ordenado de mayor a menor):

4,90000000123
4,78000008
4,69
4,67
4,64759
4,5678
4,45
4,32
4,0000786789
4,0000000000000234